基本から始める物理シミュレーション
このページでは一般的に紹介される「物体の運動」のシミュレーションではなく、もう少しミクロな 物理の振る舞いをシミュレーションしていきます。 目的とするシミュレーションは統計物理から「2次元イジングモデル」、量子力学から「ポテンシャル障壁を透過・反射する粒子」としました。
シミュレーションに使用する言語はC#としました。環境構築が楽なのと、Windowsでグラフィックの表示が楽なのが選定理由です。
0.C#の環境構築(使用ソフトのインストールとか)
インストールに関しては、このサイトでは説明を省略します。 以下のサイトを参考にして、Visual Studio 2017 Communityのインストールを行ってください。プログラミングとゲームの杜-Visual C# をインストールしよう
1.C#のコンソールアプリの作成と実行
いきなりグラフィックの出力に挑戦するのではなく、まずはテキスト出力のアプリ(コンソールアプリ)を作ります。 「ファイル」→「新規作成」→「プロジェクト」から以下の画面が開きます。出てきた画面の左側にある「インストール済み」→「Visual C#」をクリックすると、画面中央に様々なアプリの候補が出てきます。 「コンソールアプリ(.NET Framework)」を選び、プロジェクトの名前を「FirstProject」に変え、OKボタンを押します。
自動的にプロジェクト(アプリを作成するソースコード一式)が生成されます。 今回書き加えていくソースコードファイルは「Program.cs」です。初期状態ではProgram.csは以下のようになっていると思います。
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
namespace FirstProject
{
class Program
{
static void Main(string[] args)
{
}
}
}
コンソールタイプのアプリでは最初に Main 関数内の処理が実行されます。 今回は簡単な足し算と文字列の出力を行います。
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
namespace FirstProject
{
class Program
{
static void Main(string[] args)
{
int a = 10;
int b = 5;
Console.WriteLine("とりあえず文字を出力 a+bは?");
Console.WriteLine(a + b);
Console.WriteLine("次は数字と文字を同じ行に出力するよ");
Console.Write(a + b);
Console.WriteLine(" ←a+bの結果");
}
}
}
自由落下シミュレーション
まずは簡単な問題Q:自由落下運動を考える。重力加速度の大きさを$g(\mathrm{m/s^2})$としたとき、 落下し始めてから$t$秒後の、下方向を正の向きにとる変位$y(\mathrm{m})$はいくらになるか?
A:運動方程式より \begin{eqnarray} m\frac{d^2y}{dt^2} &=& mg\\ y&=&\frac{1}{2}gt^2+C_1t+C_2\\ \mbox{t=0で速度=0(m/s)}&,&\mbox{変位0(m)なので}\\ y&=&\frac{1}{2}gt^2 \end{eqnarray} $t(\mathrm{s})$後の変位をC#を用いて計算します。
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
namespace FirstProject
{
class Program
{
static void Main(string[] args)
{
double g = 9.8;//重力加速度(m/s^2)
double m = 1.3;//物体の重さ(kg)
for(int t = 0; t < 30; t++)
{
double y = g / 2.0 * t * t;//変位を計算する
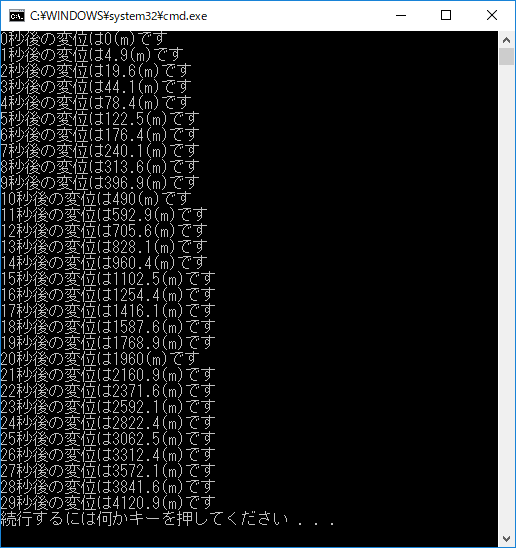
Console.WriteLine($"{t}秒後の変位は{y}(m)です");//出力
}
}
}
}
オイラー法
先ほどの計算では運動方程式を解いて$y=\frac{1}{2}gt^2$という簡単な式にしましたが、一般の問題では運動方程式が解けるとは限りません。 そこで、運動方程式などの微分方程式を近似的に解く方法が考えられました。 ここではオイラー法を用いてシミュレーションしてみます。 オイラー法の詳細は物理のかぎしっぽ-Euler法 にて図を用いて解説されているので、そちらをご覧ください。
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
namespace FirstProject
{
class Program
{
static void Main(string[] args)
{
double g = 9.8;//重力加速度(m/s^2)
double m = 1.3;//物体の重さ(kg)
double y = 0;//物体の変位(m)
double v = 0;//物体の速度(m/s)
double dt = 1;//オイラー法 計算時間刻み(s)
for (double t = 0; t < 30; t=t+dt)//for文ではtをdtずつ増やしていく
{
Console.WriteLine($"{t}秒後の変位は{y}(m)です");//出力
double newV;//t+dt秒での速度
double newY;//t+dt秒での位置
//ここからt+1秒でのパラメーターを求める
newV = v + g * dt;
newY = y+v* dt;
//新しいvとyに更新する
v = newV;
y = newY;
}
}
}
}
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
namespace FirstProject
{
class Program
{
static void Main(string[] args)
{
double g = 9.8;//重力加速度(m/s^2)
double m = 1.3;//物体の重さ(kg)
double y = 0;//物体の変位(m)
double v = 0;//物体の速度(m/s)
double dt = 0.01;//オイラー法 計算時間刻み(s)
double dtOut = 1;//出力する時間刻み(s) dtの整数倍にする
for (double t = 0; t < 30; t += dtOut)//出力用forループ
{
Console.WriteLine($"{t}秒後の変位は{y}(m)です");//出力
double tOut = t;//前回出力を行った時の時刻
for (int i = 0; i < (int)(dtOut / dt + 0.5); i++)//計算用forループ
{//dt進める処理をdtOut/dt回行うとdtOut秒進む
double newV;//t+dt秒での速度
double newY;//t+dt秒での位置
newV = v + g * dt;
newY = y + v * dt;
//新しいvとyに更新
v = newV;
y = newY;
}
}
}
}
}